| Главная » Статьи » Другие статьи. » Аэродинамика |
"Человек не имеет крыльев и по
отношению веса своего тела к весу мускулов он в 72 раза слабее
птицы…. Но я думаю, что он полетит, опираясь не
на силу своих мускулов, а на силу своего
разума." Н.Е. Жуковский Моделизмом можно заниматься по-разному. Для людей амбициозных это спорт,
соревнования и утверждение своего «Я» среди коллег. Для остальных это просто
хобби. Кто-то больше любит летать, кто-то строить самолеты. Есть еще категория
людей творческих, стремящихся не просто ходить по проторенным дорожкам, но и
пробовать, а что там, рядом, может более интересно? Это категория
конструктора-любителя. От профессионала он отличается чаще всего отсутствием
специального образования. Читать учебники по аэродинамике для «Большой» авиации
дело непростое. А привнести в модель что-то свое хочется. Экспериментировать же
наобум – малопродуктивное занятие. Из этого тупика часто раздаются возгласы:
дескать, нечего тут придумывать, все уже придумано до нас; бери Экстру и делай
по готовым чертежам. Или: нету тут никаких теорий, в моделях все – эмпирика! Не
соглашаясь ни с теми, ни с другими. Предлагаем вниманию людей творческих
введение в теорию несущего крыла. Для простоты восприятия, здесь почти нет
формул и количественных соотношений. Все зависимости даются качественно, по
принципу: данный параметр влияет на то-то в ту сторону. Это полезно знать не
только конструкторам, но и пилотам, интересующимся, почему модель в воздухе
ведет себя так, а не иначе. Заодно введем элементарную терминологию, чтобы
моделист не измерял крыло в «длину» и «ширину». Часть первая посвящена только
профилю крыла. Во второй части будут рассмотрены все остальные аспекты
аэродинамики крыла. Терминология Чтобы однозначно понимать друг–друга при рассуждениях, рассмотрим основные
понятия геометрии профиля крыла. Поперечное сечение крыла плоскостью,
параллельной плоскости его симметрии называется « профилем». Типовой профиль
крыла выглядит так:
Максимальное расстояние между крайними точками профиля – b , называется хордой профиля. Наибольшая высота профиля – c , называется толщиной профиля, а ее расстояние от
передней точки – координатой максимальной толщины. Линию, точки которой
равноудалены от верхней и нижней образующих профиля - l, называют средней
линией профиля. Ее максимальное расстояние от хорды – f, называется кривизной профиля, а удаление от передней точки – координатой максимальной кривизны. Носик
профиля образован некоей кривой линией, минимальный радиус которой обозначают –
r, это радиус скругления носика профиля. Поскольку
качественно надо сравнивать разные профили разных размеров, договорились все
указанные величины измерять относительно хорды профиля. Зачастую при этом даже
опускают слово «относительная». Просто, если толщина профиля указана в %, то
всем ясно, что это отношение реальной толщины к величине хорды профиля. На
данном рисунке верхняя линия, образующая профиль одной формы, а нижняя –
другой. Такой профиль называетсянесимметричным. Если же, одна
образующая, является зеркальным отражением другой, то профиль называетсясимметричным.
Нетрудно сообразить, что кривизна симметричного профиля равна нулю. Картина обтекания профиля Всем известно, что крыло создает подъемную силу, только тогда, когда оно
движется относительно воздуха. Т.е. характер обтекания воздухом верхней и
нижней поверхностей крыла непосредственно создает подъемную силу. Как это
происходит?
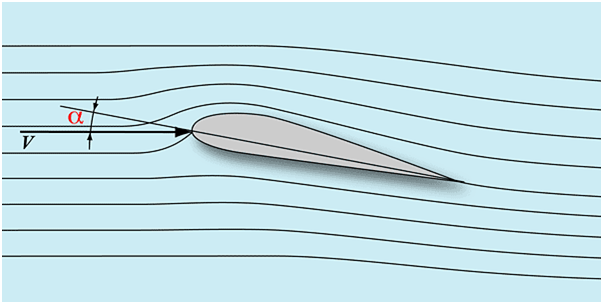
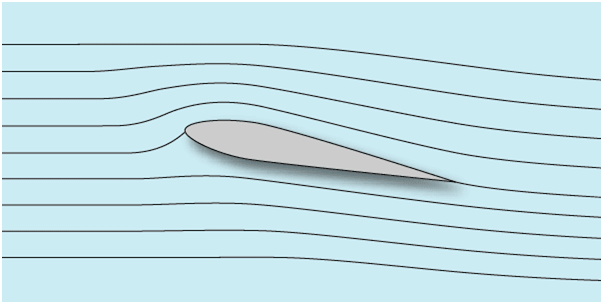
Здесь линии течения элементарных струек воздуха обозначены тонкими линиями.
Профиль к линиям течения находится под углом атаки а – это угол между хордой профиля и невозмущенными линиями течения. Там,
где линии течения сближаются, скорость потока возрастает, а абсолютное давление
падает. И наоборот, где они становятся реже, скорость течения уменьшается, а
давление возрастает. Отсюда получается, что в разных точках профиля воздух
давит на крыло с разной силой. Разницу между местным давлением у поверхности
профиля и давлением воздуха в невозмущенном потоке можно представить в виде
стрелочек, перпендикулярных контуру профиля, так что направление и длина
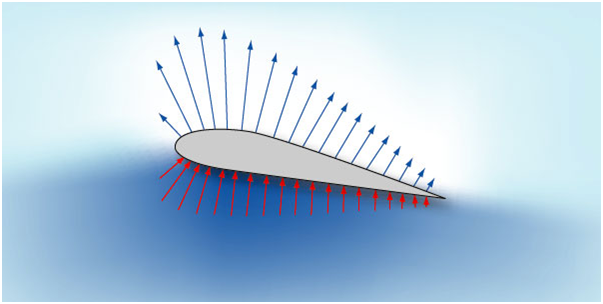
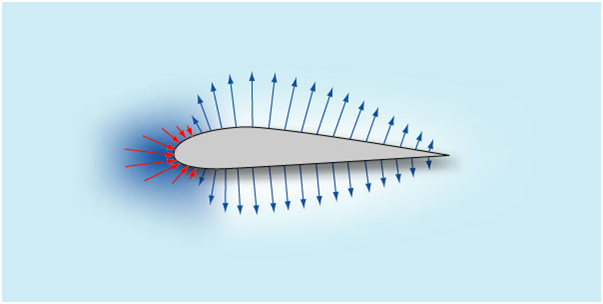
стрелочек пропорциональна этой разнице. Тогда картина распределения давления по
профилю будет выглядеть так: Здесь хорошо видно, что на нижней образующей профиля имеется избыточное
давление – подпор воздуха. На верхней же, - наоборот, разряжение. Причем оно
больше там, где выше скорость обтекания. Примечательно здесь то, что величина
разряжения на верхней поверхности в несколько раз превышает подпор на нижней.
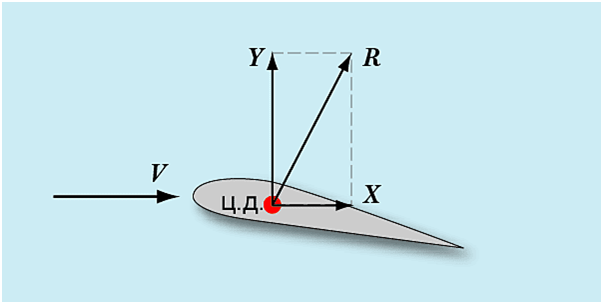
Векторная сумма всех этих стрелочек и создает аэродинамическую силу R, с которой воздух действует на движущееся крыло:
Разложив эту силу на вертикальную Yи горизонтальную X компоненты, мы
получим подъемную силу крыла и силу его лобового сопротивления. Из картины
распределения давления видно, что львиная доля подъемной силы образуется не из
подпора на нижней образующей профиля, а из разряжения на верхней, что
опровергает весьма распространенное заблуждение начинающих моделистов. Точка приложения силы R зависит от характера распределения давления по
поверхности профиля. При изменении угла атаки, распределение давления тоже
будет изменяться. Вместе с ним будет меняться и векторная сумма всех сил по
абсолютной величине, направлению и точке приложения. Кстати, последнюю называют центром давления. С ним тесно связано понятие фокуса профиля. У симметричных профилей эти точки совпадают. У несимметричных
положение центра давления на хорде при изменении угла атаки меняется, что очень
затрудняет расчеты. Чтобы их упростить, было введено понятие фокуса. При этом
равнодействующую аэродинамических сил разделили не на две компоненты, а на три
– к подъемной силе и силе лобового сопротивления добавился еще момент крыла.
Такой, вроде бы нелогичный прием позволил, поместив точку приложения подъемной
силы в фокусе профиля, зафиксировать его положение и сделать его независящим от
угла атаки. Прием удобный, только не надо забывать о появившемся при этом
моменте крыла. Разряжение на верхней части профиля можно не только измерить приборами, но
и при определенных условиях увидеть собственными глазами. Как известно, при
резком расширении воздуха, содержащаяся в нем влага может мгновенно
конденсироваться в капельки воды. Кто бывал на авиашоу, мог видеть, как во
время резкого маневрирования самолета, с верхней поверхности крыла срываются
струйки белой пелены. Это и есть водяной пар, сконденсировавшийся при
разряжении в мелкие капельки воды, которые очень быстро снова испаряются и
становятся невидимыми. Зависит ли характер обтекания от размеров профиля и фактической скорости
движения крыла относительно воздуха? Да, и очень сильно. Связано это с
физическими свойствами воздуха, главными из которых являются упругость,
плотность и вязкость. Упругость (еще говорят, сжимаемость) важна только при скоростях движения,
сопоставимых со скоростью звука. В моделизме такие скорости встречаются лишь на
концах лопастей воздушного винта. Поскольку мы занимаемся сейчас крылом, про
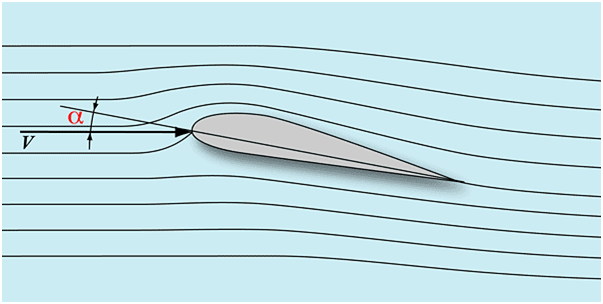
это свойство воздуха можем забыть. Массовая плотность воздуха является главной причиной возникновения
подъемной силы крыла. Уже на втором рисунке видно, что направления линий
обтекания воздуха до крыла и после него несколько не совпадают. Т.е. крыло
скашивает поток воздуха вниз. Поскольку поток обладает определенной массой, то
по закону сохранения импульса на крыло действует сила R. Отсюда следует простая
зависимость, чем воздух плотнее, тем при прочих равных условиях больше
подъемная сила. На большой высоте плотность воздуха снижается, но для моделей
это не важно, - они так высоко не летают. А вот увеличение плотности воздуха
при снижении его температуры заметно уже для моделей. Один и тот же самолет
зимой сможет выполнить петлю меньшего радиуса, чем летом. Вязкость воздуха, - словосочетание непривычное. Вязкость автомобильного
масла – это понятно, а воздуха? Тем не менее, воздух тоже обладает определенной
вязкостью. Причем причины и механизм ее возникновения такие же, как и у
автомобильного масла, только величина намного меньше. Слои воздуха движутся
друг относительно друга с трением. Очень маленьким, но не нулевым. В картине
обтекания крыла вязкость приводит к тому, что у самой поверхности профиля на
границе между твердой поверхностью и потоком воздуха возникает тоненький слой
воздуха, как бы присоединенный к крылу и движущийся вместе с крылом. Его так и
называют – пограничный слой. Поведение этого слоя
сильно зависит от размеров профиля и скорости его обтекания воздухом. Для того
чтобы оценивать степень влияния вязкости воздуха на характер обтекания крыла
при разных условиях придумали коэффициент, равный произведению хорды крыла (в
метрах) на скорость его движения относительно воздуха (в метрах в секунду),
деленному на вязкость воздуха. Называется этот коэффициент числом Рейнольдса в честь английского физика и
обозначается так: Re. В моделистских применениях вязкость воздуха можно считать
постоянной без большой погрешности и равной 0,000015 м 2/сек. Будет удобнее считать число Рейнольдса по приближенной формуле
Re=70*V*b. Здесь скорость надо подставить в метрах в секунду, а хорду в
миллиметрах. Чтобы было понятнее, приведем пример. Крыло модели планера с
хордой 0,1 метр летит со скоростью 6 метров в секунду. Получаем Re=42000. Это
очень маленькое значение для летающих моделей и характерно для свободнолетающих
моделей класса F1. При таких значениях Re вязкость имеет огромное значение.
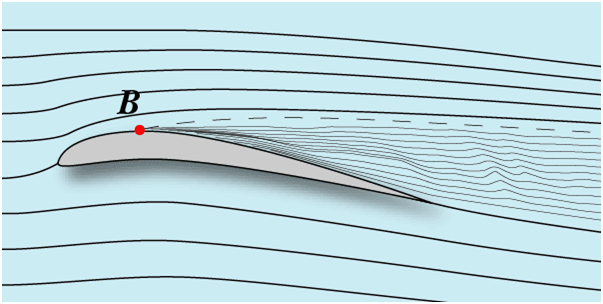
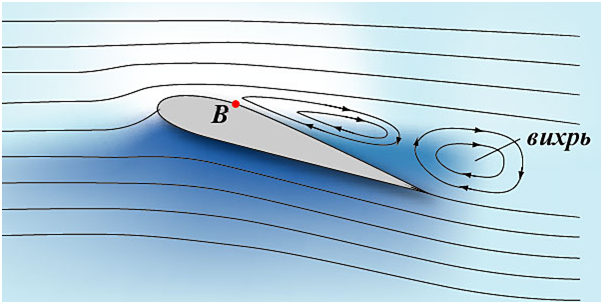
Обтекание профиля при этом выглядит так:
Здесь интересно обратить внимание на точку В. До нее течение воздуха в
пограничном слое плавное, без перемешивания прислойных струек. Такое течение
называется ламинарным. В нем практически
нет маленьких воздушных вихрей, перемешивающих воздух из соседних слоев. В
точке В начинается образование прислойных вихрей, перемешивающих воздух из
соседних слоев. Такое течение называется турбулентным. Можно так построить
форму образующей профиля, что на его большей верхней части течение воздуха
будет ламинарным, а точка В сдвинется назад по профилю. Такие профили называют ламинаризованными. Какое течение лучше для модели? Здесь однозначного ответа на все случаи
жизни нет. Ламинарное течение в сравнении с турбулентным имеет свои
преимущества и недостатки. Здесь назовем только достоинство – при ламинарном
течении трение поверхности крыла о воздух меньше. Значит и меньше лобовое
сопротивление. О недостатках ламинарного обтекания поговорим позже. Для модели пилотажки с хордой крыла 0,3 метра и скоростью 20 метров в
секунду получается Re=400000. Обтекание профиля будет выглядеть так:
Очень похоже? Да, но профиль не тот. А что будет, если планерный профиль
разогнать до этих скоростей? Или наоборот, пилотажный профиль поставить на
планер F1? Это мы рассмотрим также попозже. А сейчас посмотрим, как посчитать
подъемную силу и лобовое сопротивление крыла. Совсем обойтись без формул не получится. Да и не интересно это. Приведем
лишь две. Подъемная сила крыла: Y= Cy* p*V 2*S/2 Сила лобового сопротивления: X= Cx* p*V 2*S/2 Здесь: p - массовая плотность воздуха V - скорость движения крыла относительно воздуха S - площадь крыла Cy - коэффициент подъемной силы крыла (читается – це игрек) Cx – коэффициент лобового сопротивления крыла (читается – це икс)
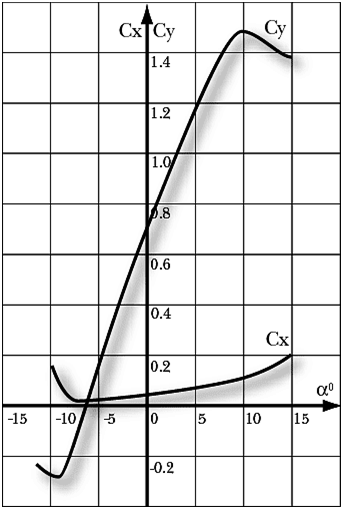
Здесь много интересного. Попробуем разобраться, почему графики идут так, а
не иначе. Начнем с нулевого угла атаки. Как видно из графика при нем подъемная
сила не равна нулю. Это связано с разными верхней и нижней образующими профиля,
т.е. с ненулевой его кривизной. Верхняя образующая более выпуклая, чем нижняя
поэтому давление распределяется так:
Чтобы подъемная сила несимметричного профиля стала бы равной нулю, его надо
расположить под отрицательным углом атаки.
В точке В происходит отрыв пограничного слоя от поверхности крыла. За
точкой отрыва возникает вихревое обтекание с линиями обратного тока. Происходит
срыв потока. При дальнейшем небольшом увеличении угла атаки Су вначале слегка
возрастает. Но точка отрыва быстро перемещается вперед по верхней образующей,
после чего Су начинает падать. Угол атаки, на котором достигается перегиб
кривой Су, называется критическим углом атаки. Теперь обратимся к Сх. При нулевой подъемной силе он минимален. Лобовое
сопротивление при этом обусловлено двумя компонентами: трением воздуха о
поверхность крыла и динамическим сопротивлением, смысл появления которого
хорошо виден на рисунке 8. Видите там стрелочки, направленные на носик профиля.
Лобовое сопротивление, состоящее из этих двух компонент, называют профильным сопротивлением. По мере увеличения угла атаки
появляется и растет подъемная сила крыла. Лобовое сопротивление при этом тоже
растет, сначала медленно, потом быстрее. Разницу между лобовым сопротивлением
при ненулевой подъемной силе и профильным сопротивлением называют индуктивным сопротивлением. Оно в широких пределах пропорционально
квадрату Су. При срыве обтекания Сх быстро растет и не убывает при дальнейшем
росте угла атаки. Обратите внимание, как изменяется Су в диапазоне отрицательных углов атаки.
Линейный рост довольно быстро заканчивается, а критический угол атаки наступает
гораздо раньше, чем при положительных углах и при намного меньшем абсолютном
значении Су. Отсюда становится понятным, почему при несимметричном профиле
крыла прямая и обратная петли самолета, столь сильно отличаются по величине
минимального радиуса. Для симметричного профиля линия Су для отрицательных углов
повторяет зеркально линию для положительных углов. Поэтому на пилотажных
самолетах применяют чаще всего симметричные профили. Аэродинамическим качеством профиля называется отношение
подъемной силы к лобовому сопротивлению. Сам термин качество происходит из
функции крыла – оно призвано создавать подъемную силу. А то, что при этом
появляется побочный эффект – лобовое сопротивление, явление вредное. Поэтому
логично отношение пользы к вреду назвать качеством. Если построить зависимость
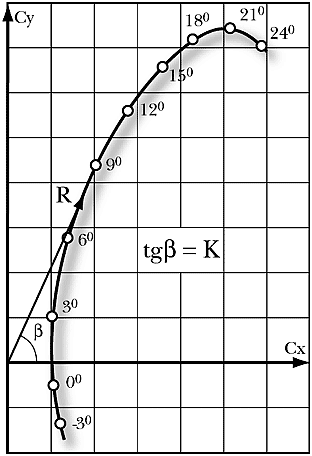
Су от Сх на графике:
то эту линию называют полярой профиля. Полярой она называется не случайно. Кто помнит из школы, что кроме
привычных прямоугольных координат, еще бывают полярные, тот быстро поймет, что
эта же кривая в полярных координатах дает зависимость длины отрезка между
началом координат и любой точкой на поляре от угла наклона этого отрезка к
горизонтальной оси. Так вот, длина отрезка пропорциональна полной
аэродинамической силе R, действующей на крыло, а тангенс упомянутого угла равен
аэродинамическому качеству К. Т.е. поляра позволяет очень просто оценивать
изменение аэродинамического качества профиля крыла. Для удобства, на кривую
принято наносить реперные точки, отмечающие соответствующий угол атаки крыла.
По поляре легко оценить профильное сопротивление, максимально достижимое
аэродинамическое качество профиля и его другие, важные параметры. Поляра
зависит от числа Re. Свойства профиля удобно оценивать по семейству поляр, построенных
в одной сетке координат для различных чисел Re. Поляры конкретных профилей получают двумя способами: 1. Продувками в
аэродинамической трубе 2. Теоретическими
расчетами. Следует заметить, что в последнее время теория, вкупе с компьютерными
достижениями, позволила создать программы рассчитывающие поляры, довольно точно
совпадающие с экспериментальными продувками. Например, весьма удобной для
любительских целей программой для построения поляр с большой базой данных по
геометрии известных профилей, является программа Profili, разработанная
итальянскими моделистами. В этой программе Су обозначается как Cl, а Сх - как
Cd. Поляра, это один из самых наглядных способов оценки свойств профиля для
конкретных применений. По этой кривой легко оценить изменение подъемной силы и
лобового сопротивления при изменении угла атаки и их соотношение, то есть
качество. По семейству поляр для разных чисел Re просто оценивается поведение
этих сил при изменении скорости. Характер кривой в диапазоне малых подъемных
сил в диапазоне скоростей показывает способность крыла разгоняться в
пикировании самолета. Кривая на больших Су показывает способность к парению на
малых скоростях, а ее плавный или резкий изгиб, характеризует темп сваливания
при срыве потока обтекания. Асимметрия и поведение поляры в районе
отрицательных Су показывает способность крыла к перевернутому полету, обратным
петлям и демонстрирует, насколько они будут отличаться от прямого полета и
прямых фигур. По семействам поляр нескольких профилей удобно проводить
сравнительный анализ их свойств и выбирать наиболее подходящий для конкретного
применения. | |
| Просмотров: 2124 | Теги: | Рейтинг: 0.0/0 |
| Всего комментариев: 0 | |